Trigonometry with Math Editor: LaTex or Braille, JAWS or NVDA

To enter college, you need a foundation in Algebra and Geometry. For STEM fields, add Calculus and Trigonometry. Trigonometry studies the relationships between angles and sides of triangles. With tools like Trigonometry with Math Editor, Braille Math Editor and screen readers, you can easily explore these relationships. It uses sine, cosine, and tangent functions to relate angles to side lengths. These functions are essential in physics, engineering, and astronomy. They help solve problems involving distances and angles. For example, trigonometry determines the height of a building or the distance across a river without direct measurement.

Trigonometry provides tools to model and solve problems involving angles and distances. It is fundamental to mathematics and its applications.

Going to College

If you go into STEM field IN college, you need advanced classes in but not limited to college algebra, trigonometry and calculus. When you are a screen reader and Braille user, these skills will allow you the options and opportunities to complete work as sighted peers.

Let’s talk about: Trigonometry which is a branch of mathematics that studies the relationships between the angles and sides of triangles

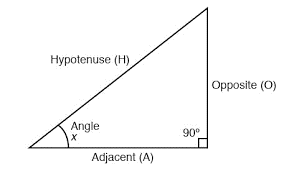
You can copy this content and paste into WORD OFFICE 365. Make sure you select Math 1 at a time and alt = to turn into true math. Then you can Ctrl = to change to professional or keep the LaTex then enter and braille it in again using Nemeth or UEB Math or practice LaTex.

Problem 1: Finding the Length of a Side

Given: A right triangle with one angle of 30° and the hypotenuse of 10 units.
Find: The length of the side opposite the 30° angle.

Solution:

1. Use the sine function:
   • \sin(30°) = \frac{\text{opposite}}{\text{hypotenuse}}sin(30°)=hypotenuseopposite​

2. Substitute the known values: \sin(30°) = \frac{x}{10}sin(30°)=10x

3. Since: \sin(30°) = 0.5sin(30°)=0.5

Then we have: 0.5 = \frac{x}{10}0.5=10x​

4. Solve for (x):

x = 10 \times 0.5 = 5x=10×0.5=5

Problem 2: Finding an Angle

Given: A right triangle with sides of 5 units (adjacent) and 12 units (opposite).
Find: The angle opposite the 12-unit side.

Solution:

1. Use the tangent function:

\tan(\theta) = \frac{\text{opposite}}{\text{adjacent}}tan(θ)=adjacentopposite​

2. Substitute the known values:

\tan(\theta) = \frac{12}{5}tan(θ)=512​

3. Use the inverse tangent function:

\theta = \tan^{-1}\left(\frac{12}{5}\right)θ=tan−1(512​)

4. Calculate the angle:

\theta \approx 67.38°θ≈67.38°

Problem 3: Finding the Hypotenuse

Given: A right triangle with legs of 6 units and 8 units.
Find: The hypotenuse.

Solution:

1. Use the Pythagorean theorem: c^2 = a^2 + b^2c2=a2+b2

2. Substitute the known values: c^2 = 6^2 + 8^2c2=62+82

3. Calculate: c^2 = 36 + 64 = 100c2=36+64=100

4. Solve for (c):

c = \sqrt{100} = 10c=100​=10

Problem 4: Finding a Side Using Cosine

Given: A right triangle with one angle of 45° and an adjacent side of 7 units.
Find: The hypotenuse.

Solution:

1. Use the cosine function:

\cos(45°) = \frac{\text{adjacent}}{\text{hypotenuse}}cos(45°)=hypotenuseadjacent​

2. Substitute the known values: \cos(45°) = \frac{7}{x}cos(45°)=x7​

3. Since: \cos(45°) = \frac{\sqrt{2}}{2}cos(45°)=22​​

Then we have: \frac{\sqrt{2}}{2} = \frac{7}{x}22​​=x7​

4. Solve for (x):

x = \frac{7 \times 2}{\sqrt{2}} = 7\sqrt{2} \approx 9.9x=2​7×2​=72​≈9.9

Problem 5: Finding an Angle Using Sine

Given: A right triangle with a hypotenuse of 13 units and an opposite side of 5 units.
Find: The angle opposite the 5-unit side.

Solution:

1. Use the sine function:

\sin(\theta) = \frac{\text{opposite}}{\text{hypotenuse}}sin(θ)=hypotenuseopposite​

2. Substitute the known values:

\sin(\theta) = \frac{5}{13}sin(θ)=135​

3. Use the inverse sine function:

\theta = \sin^{-1}\left(\frac{5}{13}\right)θ=sin−1(135​)

4. Calculate the angle:

\theta \approx 22.62°θ≈22.62°

More Math Lessons

Digital UEB Math & Braille Math Editor in WORD with JAWS UEB Mode

UEB Math using Braille Math and Word Math Editors with Jaws and split-braille-for-buffer-mode

UEB Math with NVDA in WORD using unicode-LaTex or Braille -easy to advanced math

Digital Math with UEB Math, NVDA completing Matrices in WORD Math Editor 365

JAWS or UEB Math in WORD Math Editor-Unicode-LaTex Braille=learning easy to advanced math

Quadratic Formulas with UEB Math or Nemeth and/or display with JAWS audio & MathCat

Matrices in WORD Math Editor-Braille Math editor with Jaws using LaTex, auditory and/or Braille

AI APP for Math with screen readers

Digital Quadratic Math with Jaws or NVDA in Mathkicker.ai – auditory and/or braille display

Complete Advanced Math with LaTex to finish math fast using Mathkicker.AI, JAWS, NVDA and/or display

Math & AI =Mathkicker.ai convert PDF math or any work into WORD docx.

Perfect Digital Math at all levels using only audio or tactile Braille or both in Mathkicker.ai

Math & AI is MathKicker.ai — convert to .docx from clipboard- make inaccessible accessible

Mathkicker.ai-take an image of math and make it perfect Math in Word Math editor with screen reader

Mathkicker.AI -change Math PDF to text in WORD Math editor in less than a minute with screen reader